🤔 💬 Thinking About Problems
Effectiveness of Efficiency/Avoiding Getting Stuck Techniques
In the brainstorming section of this post I came up with the following ideas for getting stuff done more efficiently and avoiding getting stuck. I wanted to share my impressions of the usefulness of my ideas:
Estimate how long you want to spend on an activity so it doesn’t become a “time sink.” If you decide you want to spend more time, that’s okay, but make this a conscious, reasoned decision as opposed to something that happens by default.
I have found this extremely helpful. Setting an estimated duration really helps with avoiding getting stuck endlessly and wasting half a day on something unproductive.
Check off things from a list of activities you want to do. Having lists helps see where you are spending your time. If you do something that isn’t on the list, add it later and check it off anyways.
This one has been okay for general tracking purposes and especially for helping to notice when I start slacking in some area (cuz stuff isn’t getting checked off).
Try switching activities for a while if you’re getting stuck or feeling low-energy.
Pretty helpful. I think I have done this before, but not as a conscious/intentional act – I have done it more by default, which is a different kind of thing.
Attitude adjustment: Take active note of things you are changing and doing differently. Give yourself credit for trying to change and improve even if you’re not seeing results as quickly as you’d like. Having a positive attitude can help with getting things done.
I’m still not very good at doing this but I’m getting better at it.
🧠 🌩 Brainstorming: Ideas on Children & Parenting I Disagree With
A list of ideas related to children and parenting that I disagree with.
1. Children are inherently irrational/can’t be reasoned with.
2. Children have inferior or undeveloped brains.
3. Children are not full human beings.
4. Children need an extended period of being dominated and controlled before they can be given freedom.
5. Children should be punished.
6. Children will learn the lesson from punishment that you intend them to learn.
7. Children should be made to keep a bed time.
8. Children should be forced to go to school.
9. Children need to be forcibly prevented from eating certain things (e.g. sweets), or else they will eat them to excess and make themselves sick.
10. Children owe their parents because the parents supported/provided for them.
11. Children should be pressured into choosing certain careers.
12. Children should be pressured into going to college.
13. Children’s “screen time” (or game-playing time, or whatever) should be limited.
14. Children should be coerced/pressured into making statements of affection for relatives.
15. Children should be uncritically taught/indoctrinated in certain perspectives (examples: left-wing politics, religious traditions, conventional social ideas – really nobody should uncritically teach anybody else anything, but parents are in a particular position of power re: being able to uncritically teach their children ideas and I think that is bad).
16. Parents should be able to veto who their children can be friends with.
17. Parents should make their kids do their homework.
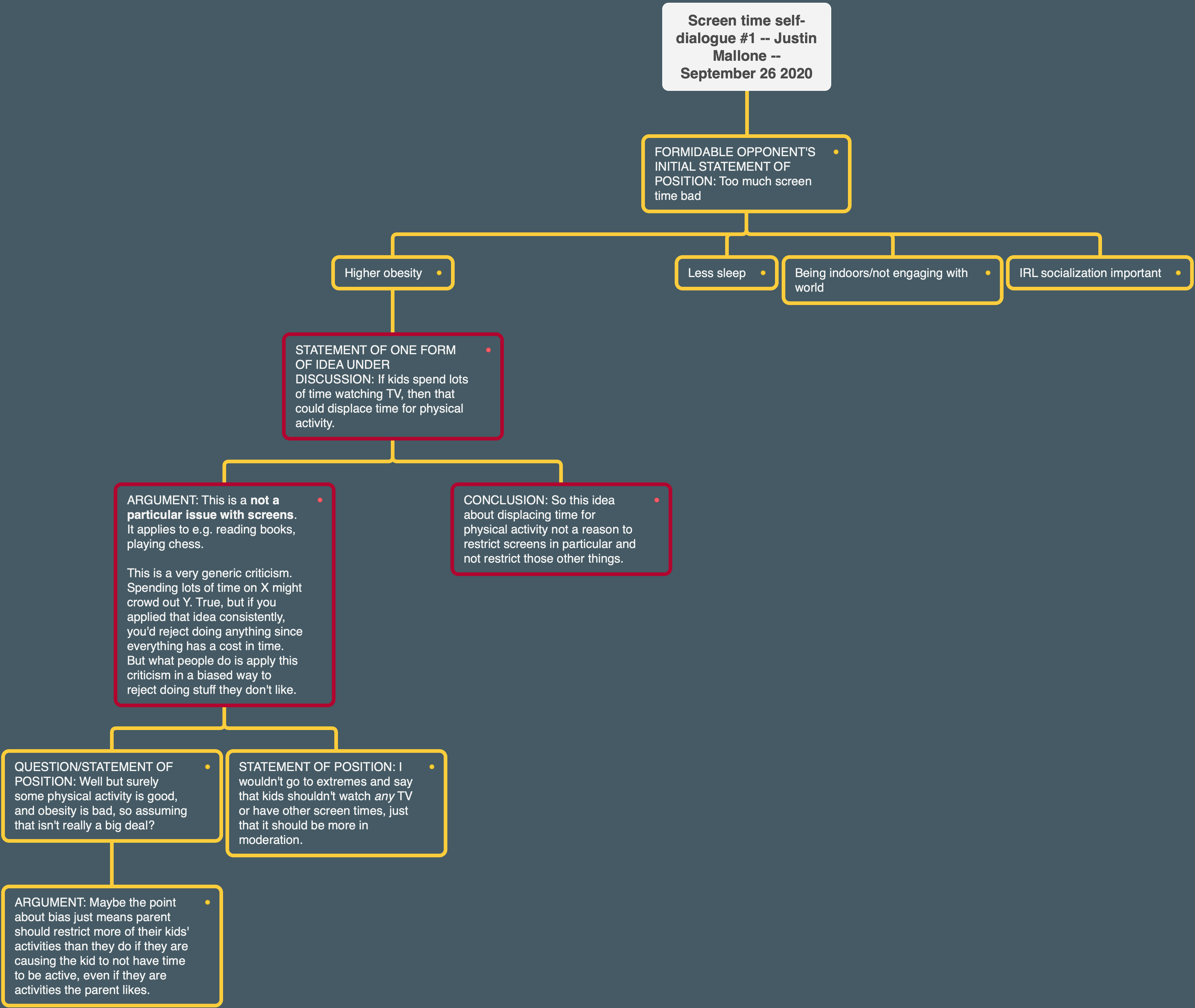
Self-Dialogue Debate: Screen-time
Justin: Hi.
Formidable Opponent: Hi. I’m in favor of screen time limits.
Justin: Why?
Formidable Opponent: I think too much screen time is unhealthy for children. There are various studies linking screen time to higher obesity, less sleep, various other problems. It’s also bad to just be indoors all the time and not engaging with the real world. Children need to socialize and live in the real world, not have all their interactions meditated through a screen.
Justin: Okay. Let’s talk about some of these detailed issues first and then try to go bigger picture. When studies talk about “linking”, I think that’s pretty vague. Let’s try to nail down the relationship a bit more.
I found this article on the web that tries to offer some explanations for the claimed link:
Researchers have hypothesized that TV watching could promote obesity in several ways: displacing time for physical activity;
So the idea is that if kids spend lots of time watching TV, then that could displace time for physical activity. This is a legitimate point but not a particular issue with screens. It basically applies to all non-physical activities, like reading books or playing chess or doing math homework.
This idea is a very generic criticism. Basically, if you spend a lot of time on some X, it might crowd out time you could spend on some Y. That’s a broadly true statement. If you try to apply this criticism consistently, though, and actually took it seriously as a reason to not do some X, you basically wind up criticizing everything on this basis, since all activities have a cost in time. So then you’d wind up doing nothing?
What I think people actually do, though, is fill in the X with the stuff they don’t like and the Y with the stuff they do like. That is biased. They are not taking their argument seriously. They’d probably evaluate the situation differently if the kids were gaining a little weight but spending lots of time on chess or violin practice instead of TV or video games.
So this idea about displacing time for physical activity not a reason to restrict screens in particular and not restrict those other things.
Formidable Opponent: I can see how people might be biased about this sort of thing and only bring up this criticism regarding stuff the dislike. However, is assuming that being obese and sedentary is bad really biased or a mistake? There are serious health issues there. Maybe the bias thing just means parents should think about this in more contexts than they do – like maybe they should be discouraging their kids from playing too much chess or doing too much reading or too much violin practice if it’s crowding out doing some physical activity.
Also I wouldn’t go to extremes and say that kids should have zero screen time, just that it should be limited.
Tree of self-dialogue so far (uses some paraphrases, not exact quotes) – Formidable Opponent in Yellow, Justin in Red
👨🏻💻 Activities
I went through some more docassemble materials and took some notes. I got a bit stuck trying to do an exercise in a video so I started reading some documentation that seemed relevant. This approach is kind of like when you get stuck in a conversation and aren’t sure how to proceed, so you just start explaining general stuff that seems relevant and hope that something clicks.
I am listening to Meditation for Fidgety Skeptics. I appreciated this quote’s perspective on standards for meditation success and rejection of the idea of clearing one’s mind:
I have heard from countless people who assume that they could never meditate because they can’t stop thinking. I cannot say this frequently enough: the goal is not to clear your mind but to focus your mind—for a few nanoseconds at a time—and whenever you become distracted, just start again. Getting lost and starting over is not failing at meditation, it is succeeding.
I think this pernicious clear-the-mind misconception stems in part from the fact that meditation has been the victim of the worst marketing campaign for anything ever. The traditional art depicting meditation, while often beautiful, can be badly misleading. It usually shows practitioners with beatific looks on their faces. Examples abound in Buddhist temples, in airport spas, and in this picture of a man in a loincloth I found on the Internet.
Based on my own practice, this image better captures the experience of meditation:
Meditation can be difficult, especially at the beginning. It’s like going to the gym. If you work out and you’re not panting or sweating, you’re probably cheating. Likewise, if you start meditating and find yourself in a thought-free field of bliss, either you have rocketed to enlightenment or you have died.