My work on https://people.eecs.berkeley.edu/~bh/ssch22/files.html
Some Brief Notes
Input/output procedures can take extra arguments to specify files, e.g.:
|
1
2
3
4
|
(show '(across the universe) file1)
(show-line '(penny lane) file2)
(read file3)
|
(so they’re all variable-argument procedures)
Scheme procedures that open a file return a port which you can use as an argument to an i/o procedure, e.g.:
|
1
2
3
4
5
6
|
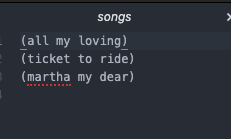
(let ((port (open-output-file "songs")))
(show '(all my loving) port)
(show '(ticket to ride) port)
(show '(martha my dear) port)
(close-output-port port))
|
I ran this and it created a songs file in the directory where I saved the scm file with the above code.
I’ve worked with files in other programming languages before (typically ruby), but not really with Scheme before!
You can read files into Scheme and deal with them there, e.g.:

If you use show-line you can make the lines in the file without parentheses:

If you want to read this file back into scheme one line at a time, you should use read-line, since just using read will do one word at a time:


They mention that closing files is important. I’ve run into the issue of forgetting to do that before.
read-string is another useful procedure:
The procedure
read-stringreads all of the characters on a line, returning a single word that contains all of them, spaces included:
Exercises
22.1 ✅❌
Write a
concatenateprocedure that takes two arguments: a list of names of input files, and one name for an output file. The procedure should copy all of the input files, in order, into the output file.
(my initial solution was very inelegant and had a conceptual misunderstanding)
My Initial (Confused & Flawed) Solution ❌
I assume they mean it should copy the content of the input files into the output file (and not just the names). This was harder than I thought it would be.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
(define (concatenate filenamelist outputname)
(let ((outp (open-output-file outputname)))
(concatenate-helper filenamelist outp)
(close-output-port outp)
'done))
(define (concatenate-helper filenamelist outp)
(if (null? filenamelist) 'done
(concatenate-helper (cdr filenamelist)
(add-single-file-to-outp (car filenamelist) outp))))
(define (add-single-file-to-outp filename outp)
(let ((file (open-input-file filename)))
(lines-from-file-to-outp file outp)
(close-input-port file)
outp
))
(define (lines-from-file-to-outp file outp)
(let ((line (read-line file)))
(if (eof-object? line)
'done
(begin (show-line line outp)
(lines-from-file-to-outp file outp))
)))
|
I realized an error in the above after looking at other people’s answers. My program still worked because of how I set it up, but was unnecessarily complicated.
I think the issue was basically that I was still thinking in terms of returning values and not in terms of causing “side effects”. So I was passing (add-single-file-to-outp (car filenamelist) outp)) as the value for the argument outp in a recursive call to concatenate-helper. And I think that was working cuz I ultimately returned outp anyways from add-single-file-to-outp… but it’s just way more elegant to call outp from within concatenate-helper from the outset…and also to use begin to make the structure clear…
Anyways I thought this was interesting. It’s a somewhat subtle thing – like my brain was still wanting to do functional programming while I was trying to learn this new style and so it came out a bit of a mess.
My Fixed Solution ✅
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
(define (concatenate filenamelist outputname)
(let ((outp (open-output-file outputname)))
(concatenate-helper filenamelist outp)
(close-output-port outp)
'done))
(define (concatenate-helper filenamelist outp)
(if (null? filenamelist) 'done
(begin (add-single-file-to-outp (car filenamelist) outp)
(concatenate-helper (cdr filenamelist) outp))))
(define (add-single-file-to-outp filename outp)
(let ((file (open-input-file filename)))
(lines-from-file-to-outp file outp)
(close-input-port file)
'done
))
(define (lines-from-file-to-outp file outp)
(let ((line (read-line file)))
(if (eof-object? line)
'done
(begin (show-line line outp)
(lines-from-file-to-outp file outp))
)))
|
You can invoke it like this (the file names are examples):
(concatenate '("songs" "songs2") "combofile")
Other Solutions
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
(define (file-concatenate infiles outfile)
(let ((outport (open-output-file outfile)))
(if (null? infiles)
'done
(map (lambda (inport) (copy-to-file inport outport)) infiles))
(close-output-port outport)))
(define (copy-to-file infile outport)
(let ((inport (open-input-file infile)))
(copy-lines inport outport)
(close-input-port inport)))
(define (copy-lines inport outport)
(let ((line (read-line inport)))
(if (eof-object? line)
'done
(begin
(show line outport)
(copy-lines inport outport)))))
|
Note the good use of map to map the lambda function to each element of infiles. That saves him the trouble of needing another helper procedure!
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
(define (concatenate files-names output-file)
(let ((out-port (open-output-file output-file)))
(concatenate-helper files-names out-port)
(close-output-port out-port)
(show-line '(>> all files are copied to the target file))
'done))
(define (concatenate-helper files-names out-port)
(if (null? files-names)
#f
(begin (copy-file (car files-names) out-port)
(concatenate-helper (cdr files-names) out-port))))
(define (copy-file file-name out-port)
(let ((in-port (open-input-file file-name)))
(copy-file-helper in-port out-port)
(close-input-port in-port)
(show-line '(one file is copied to the target file))
'done))
(define (copy-file-helper in-port out-port)
(let ((data (read in-port)))
(if (eof-object? data)
#f
(begin (show data out-port)
(copy-file-helper in-port out-port)))))
|
His structure is very similar to mine.
22.2 ✅
Write a procedure to count the number of lines in a file. It should take the filename as argument and return the number.
My Initial Solution
|
1
2
3
4
5
6
7
8
9
10
11
12
|
(define (line-counter filename)
(let ((file (open-input-file filename)))
(let ((total (line-counter-helper file 0)))
(close-input-port file)
total)))
(define (line-counter-helper file total)
(let ((line (read-line file)))
(if (eof-object? line)
total
(line-counter-helper file (+ 1 total)))))
|
Using a let for the total value in line-counter let me have something I could easily return as the final value of the procedure after closing the input port.
Reading other people’s solutions, I realized that this was unnecessarily complicated. The total value being an argument to the helper procedure is unnecessary. We do want a name that refers to the total, but we can just define that as the value returned by the helper procedure. We want a name to refer to total because we want some name we can refer to that stands for the value of the total after we’ve closed the input port for the file. We want returning the total to be the last thing in our program, and that needs to come after we’ve closed the input file port, and we can’t close the input file port until we’ve calculated the value we want. So we need to calculate that value and put it somewhere for safekeeping, and then close the input port. “Calculate that value and put it somewhere for safekeeping” is what (let ((total (line-counter-helper file))) accomplishes below in my improved solution.
Within the helper procedure, we can just add a 1 for each invocation of the helper procedure and a 0 in the base case, and then add all that up. This is what Meng Zhang did. Andrew Buntine followed much the same pattern.
My Improved Solution
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
#lang planet dyoo/simply-scheme:2:2
(define (line-counter filename)
(let ((file (open-input-file filename)))
(let ((total (line-counter-helper file)))
(close-input-port file)
total)))
(define (line-counter-helper file)
(let ((line (read-line file)))
(if (eof-object? line)
0
(+ 1 (line-counter-helper file)))))
|
After going through the above two problems, I simplified my initial answers for 22.3 and 22.4.
22.3 ✅
Write a procedure to count the number of words in a file. It should take the filename as argument and return the number.
Very similar to previous problem. I put in something to handle if there are sentences and rely on readgoing through word-by-word otherwise:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
(define (word-counter filename)
(let ((file (open-input-file filename)))
(let ((total (word-counter-helper file)))
(close-input-port file)
total)))
(define (word-counter-helper file)
(let ((element (read file)))
(cond
((eof-object? element) 0)
((sentence? element) (+ (count element) (word-counter-helper file)))
(else (+ 1 (word-counter-helper file))))))
|
This procedure is okay but can be done more simply via the method Andrew Buntine mentions. He uses length to count things up instead of my more complicated method. I was trying to be able to handle data like the following:
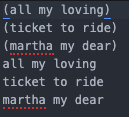
Note there are both lists (or Simply Scheme sentences) and individual words.
Andrew’s approach is able to handle this because he uses read-line to read each line, and read-line turns the lines with no parentheses around the words into lists with parentheses, thus permitting length to work correctly.
22.4 ✅
Write a procedure to count the number of characters in a file, including space characters. It should take the filename as argument and return the number.
read-string includes the spaces.
The hidden new line characters aren’t counted, unlike in things like my text editor Atom, which do count them, but I think the intent here was just to count “normal” characters anyways.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
(define (char-counter filename)
(let ((file (open-input-file filename)))
(let ((total (char-counter-helper file)))
(close-input-port file)
total)))
(define (char-counter-helper file)
(let ((element (read-string file)))
(cond
((eof-object? element) 0)
(else (+ (count element) (char-counter-helper file))))))
|
22.5 ✅
Write a procedure that copies an input file to an output file but eliminates multiple consecutive copies of the same line. That is, if the input file contains the lines

then the output file should contain

My Solution
The delete-if-exists stuff is just something I made to delete the output file if it already existed, in order to make testing faster. Hmm I should check whether Scheme has some kind of overwrite file thing.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
(define (delete-if-exists filename)
(if (file-exists? filename) (delete-file filename) 'nada))
(define (remove-dupe-lines filename outputname)
(delete-if-exists outputname)
(let ((outp (open-output-file outputname))
(file (open-input-file filename)))
(remove-dupes-helper file outp)
(close-output-port outp)
(close-input-port file)
'done))
(define (remove-dupes-helper file outp . last-line)
(let ((line (read-string file)))
(cond
((eof-object? line) 'done)
((equal? (se line) (se last-line))
(remove-dupes-helper file outp line))
(else (begin (write-string line outp)
(newline outp)
(remove-dupes-helper file outp line))))))
|
Anyways I think this is pretty straightforward. remove-dupes-helper is obviously where the action is happening. that procedure takes a variable number of arguments. it’s initialized with the input file and output file. If it gets to the end of the input file, it just returns done. If it detects a match between the current line and the last line, it recursive invokes itself without writing anything, which skips over the dupe. Otherwise, it writes the current line to the output file, adds a newline, and then invokes itself with the current line as the optional last-line argument, which gives it the information it needs to check the current line against the previous one. I use se in the check for whether the lines are equal cuz that seemed to enable it to work, whereas it wasn’t working initially.
Meng Zhang’s solution
Meng Zhang’s solution for comparison:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
(define (clean-duplicates input-file output-file)
(let ((in-port (open-input-file input-file))
(out-port (open-output-file output-file)))
(clean-duplicates-helper in-port (read-line in-port) out-port)
(close-output-port out-port)
(close-input-port in-port)
'done))
(define (clean-duplicates-helper in-port first-data out-port)
(let ((data (read-line in-port)))
(if (eof-object? data)
#f
(if (equal? first-data data)
(clean-duplicates-helper in-port first-data out-port)
(begin (show-line first-data out-port)
(clean-duplicates-helper in-port data out-port))))))
|
This is structurally pretty similar to mine but it has an improvement. In my version, I used a variable number of arguments to handle the issue of having a place to put the data from the previous line. Meng’s solution is different and more elegant. When invoking his helper function, he calls read-line with the input file, which reads that line into his first-data parameter within his helper procedure. Then, within the helper procedure, he names data, which is the result of invoking read-line on the input file. At this point the first two lines of the input file have been read into first-data and data respectively. He then checks whether data is empty. If not, he checks whether data and first-data are equal. If so, then, like in my version, he recursively calls his helper procedure without doing any writing. He uses first-data as his second argument here in the recursive call, though since they are equal values in this case, he could have used first-data or data. If first-data and data are not in fact equal, then he writes first-data to the output file and recursively calls his helper procedure with data in the place of the first-data parameter.
I think first-data would better be called previous-line or something. And data reflects the current line. Anyways, summing up, you initialize the helper procedure with the first line. Then within the helper procedure, you read the next line. If you’ve reached the end of the file, you return false. If the two lines match, you write nothing and recursively invoke the helper procedure to read the next line. If they don’t match, you write the previous line (first-data) to the output file and then recursively call the helper procedure with the current line as the argument for the previous line. Pretty elegant.
22.6 ✅
Write a
lookupprocedure that takes as arguments a filename and a word. The procedure should print (on the screen, not into another file) only those lines from the input file that include the chosen word.
My Solution
For input data like…
|
1
2
3
4
|
all my loving
ticket to ride
martha my dear
|
…the following works:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
(define (lookup filename wd)
(let ((file (open-input-file filename)))
(lookup-helper file wd)
(close-input-port file)
'done))
(define (lookup-helper file wd)
(let ((line (read-line file)))
(cond
((eof-object? line) 'done)
((member? wd (se line))
(display line)
(newline)
(lookup-helper file wd))
(else (lookup-helper file wd)))))
|
However, it won’t work for data formatted as lists like:
|
1
2
3
4
|
(all my loving)
(ticket to ride)
(martha my dear)
|
The reason it won’t work is related to how read-line works. read-line takes a line of input and returns a sentence:

But if you give it something that’s already a sentence, things get a bit weird:

I attempted to make a more robust version that could handle data formatted as lists but couldn’t figure out a good way to do it.
Other Solutions
Andrew Buntine’s solution was basically the same as mine except he (quite reasonably) used show line instead of my more manual combination of display and newline.
Meng Zhang’s solution had a more interesting difference. He used read instead of read-line to read the data from the input file. Because read will grab an entire line if it’s a list/sentence but only one word if the words are not surrounded by parentheses, his version works on files where the words are surrounded by parentheses, but won’t work if they’re not surrounded by parentheses. So it’s like the opposite of mine.
22.7 ❌
Write a
pageprocedure that takes a filename as argument and prints the file a screenful at a time. Assume that a screen can fit 24 lines; your procedure should print 23 lines of the file and then a prompt message, and then wait for the user to enter a (probably empty) line. It should then print the most recent line from the file again (so that the user will see some overlap between screenfuls) and 22 more lines, and so on until the file ends.
My initial solution did not solve the problem due to failing to print one a line each cycle of lines.
My Initial Solution (Flawed) ❌
Note that I also made the program output the number of the current line.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
(define (page filename)
(let ((file (open-input-file filename)))
(page-helper file 23)
(close-input-port file)
'done))
(define (page-helper file lines-to-display . last-line)
(let ((line (read-string file)))
(cond
((eof-object? line) 'done)
((= lines-to-display 1)
(display "1: ")
(show line)
(page-helper file 0 line))
((= lines-to-display 0)
(show "Type Enter to continue :")
(read-line)
(display "23: ")
(show last-line)
(page-helper file 22))
(else
(display (word lines-to-display " "))
(show line)
(page-helper file (- lines-to-display 1))))))
|
I realized that this was actually skipping over some content. It was an off-by-one type of thing where I wasn’t print one of the lines for each cycle of line printing. After glancing at some other people’s solutions and thinking about it, I tried again and came up with some simpler and better-organized code.
Corrected Solution ✅
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
(define (page filename)
(let ((file (open-input-file filename)))
(page-helper file 23)
(close-input-port file)
'done))
(define (page-helper file lines-to-display)
(let ((line (read-string file)))
(cond
((eof-object? line) 'done)
((= lines-to-display 1)
(end-of-page-helper line)
(page-helper file 22))
(else
(display (word lines-to-display " "))
(show line)
(page-helper file (- lines-to-display 1))))))
(define (end-of-page-helper line)
(display "1: ")
(show line)
(display "Type Enter to Continue: ")
(read-line)
(display "23: ")
(show line))
|
I realized I didn’t actually need to keep track of the previous line and the current line – when I got to the end of a page, I just needed to print the current line twice – before and after the user provides input.
22.8 ✅
A common operation in a database program is to join two databases, that is, to create a new database combining the information from the two given ones. There has to be some piece of information in common between the two databases. For example, suppose we have a class roster database in which each record includes a student’s name, student ID number, and computer account name, like this:

We also have a grade database in which each student’s grades are stored according to computer account name:

We want to create a combined database like this:
in which the information from the roster and grade databases has been combined for each account name.
Write a programjointhat takes five arguments: two input filenames, two numbers indicating the position of the item within each record that should overlap between the files, and an output filename. For our example, we’d say
In our example, both files are in alphabetical order of computer account name, the account name is a word, and the same account name never appears more than once in each file. In general, you may assume that these conditions hold for the item that the two files have in common. Your program should not assume that every item in one file also appears in the other. A line should be written in the output file only for the items that do appear in both files.
My solution:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
(define (join inputname1 inputname2 pos1 pos2 outputname)
(let ((outputfile (open-output-file outputname))
(file1 (open-input-file inputname1))
)
(join-helper file1 inputname2 pos1 pos2 outputfile)
(close-output-port outputfile)
(close-input-port file1)
'done))
(define (join-helper file1 inputname2 pos1 pos2 outputfile)
(let ((line1 (read file1)))
(let ((lookup-value (lookup inputname2 (overlapword line1 pos1))))
(cond
((eof-object? line1) 'done)
((equal? lookup-value '(no match found))
(write line1 outputfile)
(display " " outputfile)
(write "ERROR: no matching merge data found in second file" outputfile)
(newline outputfile)
(join-helper file1 inputname2 pos1 pos2 outputfile))
(else (begin (write (line-joiner line1 lookup-value pos1 pos2) outputfile)
(newline outputfile)
(join-helper file1 inputname2 pos1 pos2 outputfile)))))))
(define (lookup filename wd)
(let ((file (open-input-file filename)))
(let ((helper-value (lookup-helper file wd)))
(close-input-port file)
helper-value)))
(define (lookup-helper file wd)
(let ((line (read file)))
(cond
((eof-object? line) '(no match found))
((member? wd line)
line)
(else (lookup-helper file wd)))))
(define (overlapword line pos)
(if (eof-object? line) 'done
(item pos line)))
(define (line-joiner f1line f2line pos1 pos2)
(append ((repeated bl (- (count f1line) pos1))
f1line)
((repeated bf pos2)
f2line)
))
|
join opens (and ultimately closes) an output port for the output file and an input port for the first file, and invokes join-helper.
lookup and its helper return the line within the second file, if any, that contains the same value that is present in the first file at pos1. If no such line exists, lookup returns ‘(no match found). line-joiner takes two lines and the positions and joins the lines together at the indicated positions.
join-helper reads a line from the first file. Then it gets the value returned by lookup for that line, and stores it in the name lookup-value. If that value is (no match found), my code for that situation kicks in. I didn’t think it was clearly specified what to do in this case so I decided to handle it in the following way: the current line from the first file is written to the output file, and an error message “ERROR: no matching merge data found in second file” is appended to the same line to indicate that no match was found. The output looks like this:
![]()
If, on the other hand, the lookup-value is anything else, then the value returned by invoking line-joiner is written to the output file, along with a newline.
I would have used item directly in the let statement for lookup-value, but without something like overlapword that explicitly returned something when the argument to it was an eof-object, i was getting errors.
Note that each call to lookup by each recursive call of join-helper opens up a separate instance of the second file that the procedure can search through. That’s part of what makes this solution work.
