Notes
Tentatively, this may be my last Simply Scheme post. There are a couple of more chapters, but this appears to the last chapter that introduces major new conceptual material, and I’d like to try SICP again. I’m also going to have fewer answers to compare my own answers to past chapter 23, as that’s where Andrew Buntine’s answers stop.
I may take a brief break as I’m considering moving to the Ghost blogging platform. If I do do that, all my existing posts from this blog will still be up on an archive on this website.
General Notes
State is record of certain results of past interaction with you, like names of variables you’ve defined in Scheme, or characters in a text editor. This chapter is about writing programs with state using vectors, or arrays.
The book draws a distinction between state, which consists of longer term “memory” of past actions/events, and a program simply remembering an argument while it’s running or the definition of a let, which is required just for the arguments to affect the computation. They give a good example:
Suppose somebody asks you, “Car 54 has just completed a lap; how many has it completed in all?” You can’t answer that question with only the information in the question itself; you have to remember earlier events in the race. By contrast, if someone asks you, “What’s the plural of `book’?” what has happened in the past doesn’t matter at all.
vector is a constructor.

vector-length gets the length.
equal? works on vectors.
vector? works like how you think it would.
lap
First thing they want to do to is to make a lapprocedure that keeps track of the laps a car with a given (index) number has made in a race.

This is their solution for making the vector:

In the first part,
|
1
2
|
(define *lap-vector* (make-vector 100))
|
the vector lap-vector is initialized with 100 index values representing different cars. There are no values yet set inside these vectors.
initialize-lap-vector sets the initial values within the indexes of the vector to 0.
Now we can write lap:

lap is given a number representing a car. That value is used by vector-set! to set a new number of laps for the car, and by vector-ref to retrieve the existing number of laps for the car (in the course of vector-set setting the new value). The new value is then returned as the final value of the procedure.
shuffle


shuffle! takes a vectorized list of cards and an index value as arguments. if the index value drops below 0, it returns the deck. Otherwise, it invokes vector-swap! on with the following arguments: the vector/deck representing the list of cards, the index value (index1 in the vector-swap! procedure) and a random number in the range of 0 to the current index value minus 1 (index2 in the vector-swap! procedure). Note that random starts at 0, so if you give it 1 as an argument it will always return 0, if you give it 2 as an argument it return either 0 or 1, and so on.
vector-swap! defines temp as the value returned by invoking vector-ref on the list of cards with index1. It then sets the value in the vector at index1 to the value at index2, and vice-versa. Defining the temp value serves the purpose of permitting the value of (vector-ref vector index1) to be stored somewhere safe while the swap is performed. Since the equivalent for value for index2 is swapped into place first, there’s no need to store it, but if we didn’t store the temp value, then after the (vector-set! vector index1 (vector-ref vector index2)) line we would have destroyed the value we want to swap and have no way to get it.
The index is set to 51 initially, which is the end of the vector – the last card in the deck. index1 represents the last card in the portion of the deck we’re looking at (which decreases by 1 with each recursive call to shuffle!, as we work our way from back to front in the deck). The line (vector-set! vector index1 (vector-ref vector index2)) thus makes the value of the randomly selected card the value of that last card. So say the last card of the unshuffled hand is CK as in the book’s example. The procedure swaps the position of that CK with that of a randomly selected card, and then moves on to CQ, and CJ, and then works its way back ultimately all the way to HA before returning the shuffled deck.
Exercises
Do not solve any of the following exercises by converting a vector to a list, using list procedures, and then converting the result back to a vector.
23.1 ✅
Write a procedure
sum-vectorthat takes a vector full of numbers as its argument and returns the sum of all the numbers:
My answer:
|
1
2
3
4
5
6
7
8
|
(define (sum-vector vector-num)
(sum-vector-helper vector-num (vector-length vector-num) 0))
(define (sum-vector-helper vector-num vec-length index)
(if (= index vec-length) 0
(+ (vector-ref vector-num index)
(sum-vector-helper vector-num vec-length (+ 1 index)))))
|
23.2 ✅
Some versions of Scheme provide a procedure
vector-fill!that takes a vector and anything as its two arguments. It replaces every element of the vector with the second argument, like this:

Write
vector-fill!. (It doesn’t matter what value it returns.)
My initial version 1) used “vector” as the name of an argument, which is suboptimal because we don’t want to mix things up with the procedure of the same name, 2) passed vector-length as an argument from the initial procedure to the helper procedure, which was unnecessary, and 3) returned done instead of vec. It worked though, and I consider this issues more stylistic than fundamental. Below is a cleaned up version:
|
1
2
3
4
5
6
7
8
|
(define (vector-fill2! vec fill-value)
(fill-helper vec fill-value 0))
(define (fill-helper vec fill-value index)
(if (= index (vector-length vec)) vec
(begin (vector-set! vec index fill-value)
(fill-helper vec fill-value (+ 1 index)))))
|
23.3 ✅
Write a function
vector-appendthat works just like regularappend, but for vectors:
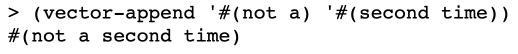
This was harder than I thought it’d be. Here was my first crack at it. I’m sure there is a better way:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
(define (vector-append vec1 vec2)
(let ((combined-length (+ (vector-length vec1)(vector-length vec2))))
(let ((newvec (make-vector combined-length)))
(append-helper vec1 vec2 newvec))))
(define (append-helper vec1 vec2 newvec)
(let ((vec1tonewvec (copy-vec vec1 newvec 0 0 (vector-length vec1)))
(combined-length (+ (vector-length vec2)(vector-length vec1))))
(let ((starting-index (- combined-length (vector-length vec2))))
(copy-vec vec2 vec1tonewvec 0 starting-index (vector-length vec2)))))
(define (copy-vec oldvec newvec oldvecindex newvecindex remaining)
(if (= remaining 0) newvec
(begin (vector-set! newvec newvecindex (vector-ref oldvec oldvecindex))
(copy-vec oldvec newvec (+ 1 oldvecindex) (+ 1 newvecindex) (- remaining 1)))))
|
Note that, within append-helper, the let for vec1tonewvec essentially copies vec1 to the newvec using copyvec. This is the first invocation of copyvec. Then that new vector, containing the copied over bits of vec1 and some “empty” slots for the content of vec2, is passed to copy-vec as the newvec for that procedure, with vec2 being passed as the old vector. And the final trick is that, for this second invocation of copy-vec, we pass a value, starting-index, that represents the difference between the combined length of the two vectors and the length of vec2. This starting-index value becomes the newvecindex within copy-vec. This places the value at which we start adding the entries from vec2 to the new combined vector at an appropriate place within the new vector. We don’t want to overwrite any of the existing content from vec1 in that new vector, and starting-index helps us accomplish that.
I looked at other people’s solutions for this problem. Meng Zhang’s appeared to be very similar in basic concept.
OTOH, Andrew Buntine’s was entirely different. He actually violated the instructions though. The instructions were
Do not solve any of the following exercises by converting a vector to a list, using list procedures, and then converting the result back to a vector.
But that’s what he did (he converts a vector to a list and winds up using append on it.) If you do that, you can make a more succinct solution. But if you want to deal purely with vectors, it’s more work.
23.4 ✅
Write
vector->list.
|
1
2
3
4
5
6
7
|
(define (myvector->list vec)
(v2lst-helper vec 0 '()))
(define (v2lst-helper vec index lst)
(if (= index (vector-length vec)) lst
(v2lst-helper vec (+ 1 index) (cons (vector-ref vec index) lst))))
|
23.5 ✅
Write a procedure
vector-mapthat takes two arguments, a function and a vector, and returns a new vector in which each box contains the result of applying the function to the corresponding element of the argument vector.
|
1
2
3
4
5
6
7
8
9
10
|
(define (vector-map fn vec)
(vmap-helper fn vec 0 (make-vector (vector-length vec))))
(define (vmap-helper fn oldvec index newvec)
(if (= index (vector-length oldvec)) newvec
(begin
(vector-set! newvec index (fn (vector-ref oldvec index)))
(vmap-helper fn oldvec (+ 1 index) newvec))))
|
23.6 ✅
Write a procedure
vector-map!that takes two arguments, a function and a vector, and modifies the argument vector by replacing each element with the result of applying the function to that element. Your procedure should return the same vector.
|
1
2
3
4
5
6
7
8
9
10
|
(define (vector-map! fn vec)
(vmap-helper fn vec 0))
(define (vmap-helper fn vec index)
(if (= index (vector-length vec)) vec
(begin
(vector-set! vec index (fn (vector-ref vec index)))
(vmap-helper fn vec (+ 1 index)))))
|
23.7 ✅
Could you write
vector-filter? How aboutvector-filter!? Explain the issues involved.
For vector-filter, well you’d need to know the length of the new vector with only the values for which the function returns true. So maybe you could run through the old vector once with, say, a counter that increases if the value is true for the function, and then make a new vector equal to the size of the counter, and then run through the old vector again and actually add the true values into the new function. Here’s a solution based on that approach:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
(define (vector-filter fn vec)
(let ((truecount (true-counter fn vec 0 (vector-length vec) 0)))
(filter-helper fn vec 0 0 (vector-length vec) (make-vector truecount))))
(define (filter-helper fn oldvec oldvecindex newvecindex vlen newvec)
(cond ((= oldvecindex vlen) newvec)
((fn (vector-ref oldvec oldvecindex))
(vector-set! newvec newvecindex (vector-ref oldvec oldvecindex))
(filter-helper fn oldvec (+ 1 oldvecindex) (+ 1 newvecindex) vlen newvec))
(else (filter-helper fn oldvec (+ 1 oldvecindex) newvecindex vlen newvec))))
(define (true-counter fn vec index vlen truecount)
(if (= index vlen) truecount
(if (fn (vector-ref vec index))
(true-counter fn vec (+ 1 index) vlen (+ 1 truecount))
(true-counter fn vec (+ 1 index) vlen truecount))))
|
For vector-filter!, which I assume would try to “filter” values within the existing vector, we haven’t been shown a way to remove/delete vectors, so I’m not sure how you’d do it. Like you could replace the vector values that return false with something else, but that’s different than just returning a vector with only the true values.
23.8 ✅
Modify the
lapprocedure to print “Car 34 wins!” when car 34 completes its 200th lap. (A harder but more correct modification is to print the message only if no other car has completed 200 laps.)
Here’s my solution to the harder one:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
(define (lap car-number)
(if (and (none-200-or-greater? *lap-vector* 0 (vector-length *lap-vector*))
(= (vector-ref *lap-vector* car-number) 199))
(begin (vector-set! *lap-vector*
car-number
(+ (vector-ref *lap-vector* car-number) 1))
(show (se "Car" car-number "wins!")))
(begin (vector-set! *lap-vector*
car-number
(+ (vector-ref *lap-vector* car-number) 1))
(vector-ref *lap-vector* car-number))))
(define (none-200-or-greater? vector index vlen)
(cond ((= vlen index) #t)
((>= (vector-ref vector index) 200) #f)
(else (none-200-or-greater? vector (+ 1 index) vlen))))
|
Basic logic of my solution is:
1. If, before any changes to any vector values are made, it is the case that a) there are no cars with a lap count of 200 or greater, and that b) the lap count of the current car number that we’re incrementing is 199, then
2. do the first-car-to-200-laps stuff. Otherwise,
3. Do the normal stuff
Andrew Buntine’s solution has a similar idea but he implements it a bit differently. The structure of his program is:
- Define a *total-laps* number of laps
- Increase the lap count of the current car by 1
- give the name lap-number to the lap value of the current car, said value having been increased by 1
- if a) the lap-number is equal to *total-laps* and 2) there are no other car numbers equal to or greater than *total-alps*, then
- do the first-car-to-the-total-laps stuff. Otherwise
- Do the normal stuff
He has a procedure, already-a-winner?, which (unsurprisingly) checks if there is already a winner. One detail worth noting is that he passes in as an argument (with the formal parameter name ignore-car) the number of the car that we’re currently incrementing, for the specific purpose of ensuring that his helper procedure doesn’t return that there is already-a-winner when considering the current car under investigation. Given how I solved the problem – where I checked for existing winners before incrementing the current car number’s value – I didn’t have to worry about this concern.
Meng Zhang’s solution seems to follow a similar pattern.
23.9 ✅
Write a procedure
leaderthat says which car is in the lead right now.
Note that I made this so that it could handle a lap-vector of any size and threw in a descriptive message at the end along with returning the car in the lead.
|
1
2
3
4
5
6
7
8
9
10
11
|
(define (leader vector)
(leader-helper vector (vector-length vector) 0 0))
(define (leader-helper vector vector-length index leader-index)
(if (= index vector-length) (begin (show (se '(Car) leader-index '(is in the lead with) (vector-ref vector leader-index) '(laps))) leader-index)
(let ((vec-val (vector-ref vector index))
(leader-val (vector-ref vector leader-index)))
(if (> vec-val leader-val)
(leader-helper vector vector-length (+ 1 index) index)
(leader-helper vector vector-length (+ 1 index) leader-index)))))
|

23.10 ✅
Why doesn’t this solution to Exercise 23.9 work?
|
1
2
3
4
5
6
7
8
9
|
(define (leader)
(leader-helper 0 1))
(define (leader-helper leader index)
(cond ((= index 100) leader)
((> (lap index) (lap leader))
(leader-helper index (+ index 1)))
(else (leader-helper leader (+ index 1)))))
|
Mechanical/detailed explanation
Calling lap actually increases the lap count on whatever index is used. From the initial state of the vector – when all the lap counts are 0 – it thus returns 1 for (lap index). The initial value of index is 1, so this sets the lap count for index/car number 1 to 1. (lap leader) likewise returns 1. The initial leader value is 0, so this sets the lap count of index/car number 0 to 1. Since 1 is equal to 1, the first condition, (lap index) (lap leader)), does not hold, and thus we recursively call leader-helper with the current leader, which is 0, and the index increased by 1, to 2. In this first recursive call, (lap index) will still return 1, whereas (lap leader) will return 2, so the condition (> (lap index) (lap leader)) will again not hold. This process will repeat 99 times, until the leader value is returned when the procedure’s index value is equal to 100.
Suppose some index’s value has been set to more than 0 before we invoke leader. Suppose, for example, that we have set index 2 to 4, but that all the other values are still 0 initially. Upon arriving at index 2, the (> (lap index) (lap leader)) condition will be true, and the procedure will recursively call itself with 2 as the value for leader and increase the index. The same pattern as before will then resume itself – the leader, index 2, will return a value that is greater than all the other indexes, and this value will be increased with each call.
If, say, car 75 had already completed 50 laps, and the leader procedure was run, by the time it got to checking car 75, because of all the calls to lap and subsequent increases of the value of car number/index 0, the procedure would think that car 0 already had a number well in excess of 50 laps, and would erroneously keep car 0 as the leader.
Summary explanation
The intended purpose of the procedure is to detect and compare the existing state of the cars in order to ascertain the leader, but in attempting to do so, the procedure actually changes the state of the cars and thus corrupts the data set it’s supposed to be merely investigating.
23.11 ✅
In some restaurants, the servers use computer terminals to keep track of what each table has ordered. Every time you order more food, the server enters your order into the computer. When you’re ready for the check, the computer prints your bill.
You’re going to write two procedures,
orderandbill.Ordertakes a table number and an item as arguments and adds the cost of that item to that table’s bill.Billtakes a table number as its argument, returns the amount owed by that table, and resets the table for the next customers. (Yourorderprocedure can examine a global variable*menu*to find the price of each item.)

Answer:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
(define (*menu* food)
(cond ((equal? food 'potstickers) 6)
((equal? food 'wor-won-ton) 4)
((equal? food 'egg-rolls) 2.75)
((equal? food 'shin-shin-special-prawns) 3.85)
(else 0)))
(define *table-vector* (make-vector 6 0))
(define (order table food)
(let ((bill-so-far (vector-ref *table-vector* table)))
(vector-set! *table-vector* table (+ (*menu* food) bill-so-far))))
(define (bill table)
(let ((total (vector-ref *table-vector* table)))
(vector-set! *table-vector* table 0)
total))
|
I define total in bill before setting the table’s value to 0 so that the value of the table is safely stored away somewhere and can be returned after i reset the table’s total.
Other solutions I saw made a list of dish names/prices and used assoc rather than what I did.
23.12 ✅
Rewrite selection sort (from Chapter 15) to sort a vector. This can be done in a way similar to the procedure for shuffling a deck: Find the smallest element of the vector and exchange it (using
vector-swap!) with the value in the first box. Then find the smallest element not including the first box, and exchange that with the second box, and so on. For example, suppose we have a vector of numbers:
![]()
Your program should transform the vector through these intermediate stages:

Testing my solution:
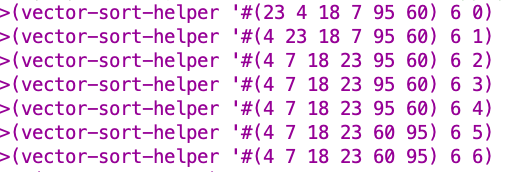
Looking good 🙂
My solution:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
(define (vector-sort vec)
(vector-sort-helper vec (vector-length vec) 0))
(define (vector-sort-helper vec vlen index)
(if (= index vlen) vec
(begin (vector-swap! vec index (smallest-element vec index))
(vector-sort-helper vec vlen (+ 1 index)))))
(define (smallest-element vec index)
(smallest-element-helper vec index (vector-ref vec index) index))
(define (smallest-element-helper vec index current-champ-value current-champ-index)
(if (= (+ 1 index) (vector-length vec)) current-champ-index
(let ((new-contender-value (vector-ref vec (+ 1 index))))
(cond
((< current-champ-value new-contender-value)
(smallest-element-helper vec (+ 1 index) current-champ-value current-champ-index))
(else (smallest-element-helper vec (+ 1 index) new-contender-value (+ 1 index)))))))
(define (vector-swap! vector index1 index2)
(let ((temp (vector-ref vector index1)))
(vector-set! vector index1 (vector-ref vector index2))
(vector-set! vector index2 temp)))
|
smallest-element is the tricky part here. It returns the index value of the smallest element within the range being looked at and hands it off to vector-swap! smallest-element works by taking a current-champ-value and comparing it to a new contender and seeing if the current champ is smaller than the new contender.
(Note: I could have made this more elegant by not defining names of the values and just using the indexes within a call to vector-ref and comparing those results directly, as Meng Zhang does here. It helped me conceptually to think about comparing the values but the code could have been simplified).
Here is a “long” version I made with a bunch of show statements to help make sure that my procedure was working how I wanted it to:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
(define (vector-sort vec)
(vector-sort-helper vec (vector-length vec) 0))
(define (vector-sort-helper vec vlen index)
(if (= index vlen) vec
(begin (vector-swap! vec index (smallest-element vec index))
(vector-sort-helper vec vlen (+ 1 index)))))
(define (smallest-element vec index)
(smallest-element-helper vec index (vector-ref vec index) index))
(define (smallest-element-helper vec index current-champ-value current-champ-index)
(begin (show (se "the current champ is: " current-champ-value))
(if (= (+ 1 index) (vector-length vec)) current-champ-index
(let ((new-contender-value (vector-ref vec (+ 1 index))))
(begin (show (se "the new contender value is: " new-contender-value))
(cond
((< current-champ-value new-contender-value)
(begin (show (se "the current champ beats the new contender"))
(smallest-element-helper vec (+ 1 index) current-champ-value current-champ-index)))
(else (begin (show (se "the new contender beats the current champ")))
(smallest-element-helper vec (+ 1 index) new-contender-value (+ 1 index)))))))))
(define (vector-swap! vector index1 index2)
(let ((temp (vector-ref vector index1)))
(vector-set! vector index1 (vector-ref vector index2))
(vector-set! vector index2 temp)))
(trace vector-sort)
(trace vector-sort-helper)
(trace vector-swap!)
(trace smallest-element)
(trace smallest-element-helper)
|
BTW I kept getting error messages when I tried to Dr Racket so I used this workaround to get the procedure to take the vector:
![]()
23.13 ✅
Why doesn’t this work?

I explained this earlier in the section on shuffle. Basically, if you don’t define a temp value with the value of the vector at index1, then when you “swap” the value at index2 into the slot at index1, then you’ve destroyed the value that was in index1. You haven’t put the value at index1 anywhere, and now you’ve got two copies of the value at index2, so where are you gonna get the value that was at index1 from to finish the swap?
23.14 ✅
Implement a two-dimensional version of vectors. (We’ll call one of these structures a matrix.) The implementation will use a vector of vectors. For example, a three-by-five matrix will be a three-element vector, in which each of the elements is a five-element vector. Here’s how it should work:

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
(define (make-matrix a b)
(make-for-each (make-vector a) b 0))
(define (make-for-each vec vec-depth index)
(if (= index (vector-length vec))
vec
(begin (vector-set! vec index (make-vector vec-depth))
(make-for-each vec vec-depth (+ 1 index)))))
(define (matrix-set! mat a b val)
(vector-set! (vector-ref mat a) b val))
(define (matrix-ref mat a b)
(vector-ref (vector-ref mat a) b))
|
23.15 ✅
Generalize Exercise 23.14 by implementing an array structure that can have any number of dimensions. Instead of taking two numbers as index arguments, as the matrix procedures do, the array procedures will take one argument, a list of numbers. The number of numbers is the number of dimensions, and it will be constant for any particular array. For example, here is a three-dimensional array (4×5×6):

Answer:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
(define (make-array lst)
(make-array-helper (make-vector (car lst)) (cdr lst)))
(define (make-array-helper vec lst)
(if (null? lst) vec
(make-array-helper (find-vec-elem-and-apply-fn vec (lambda (elem) (make-vector (car lst))) 0)
(cdr lst))))
(define (array-set! arr lst val)
(array-set-helper (vector-ref arr (car lst)) (cdr lst) val))
(define (array-set-helper arr lst val)
(if (null? (cdr lst)) (vector-set! arr (car lst) val)
(array-set-helper (vector-ref arr (car lst)) (cdr lst) val)))
(define (array-ref arr lst)
(array-ref-helper (vector-ref arr (car lst)) (cdr lst)))
(define (array-ref-helper arr lst)
(if (null? (cdr lst)) (vector-ref arr (car lst))
(array-ref-helper (vector-ref arr (car lst)) (cdr lst))))
(define (find-vec-elem-and-apply-fn vec fn index)
(if (= index (vector-length vec)) vec
(if (vector? (vector-ref vec index))
(begin (find-vec-elem-and-apply-fn (vector-ref vec index) fn 0)
(find-vec-elem-and-apply-fn vec fn (+ 1 index)))
(apply-fn-to-vec-elems vec fn 0))))
(define (apply-fn-to-vec-elems vec fn index)
(if (= index (vector-length vec)) vec
(begin (vector-set! vec index (fn (vector-ref vec index)))
(apply-fn-to-vec-elems vec fn (+ 1 index)))))
|
The interesting part of this, IMHO, is find-vec-elem-and-apply-fn and apply-fn-to-vec-elems. These procedures “dig” through a vector to find the elements of the vector and then apply a function. Within make-array-helper, I hand find-vec-elem-and-apply-fn a lambda procedure that takes make-vector and returns a procedure that makes a vector of a given size (based on the input in the input list). The vector that results from that process is then passed to make-array-helper as an argument – the new vector to which it should repeat the same process for the next value in the input lst. By this means, we can create vectors with arbitrary numbers of dimensions.
For example, using the above procedures and then running:
|
1
2
3
|
(define a1 (make-array '(4 5 6)))
(array-set! a1 '(3 2 3) '(the end))
|
we get the following as the value of a1:

(remember that vectors have 0 indexes if you’re confused about the placement of (the end)).
23.16 ✅🤔
(some of my responses are a bit tentative and I’m not sure I “did it right”, but I figured some stuff out and seemed to get the right outputs. If anyone sees any errors though, lemme know).
We want to reimplement sentences as vectors instead of lists.
(a) Write versions ofsentence,empty?,first,butfirst,last, andbutlastthat use vectors. Your selectors need only work for sentences, not for words.

sentence in vectors:
|
1
2
3
|
(define (vec-sentence arg1 . rest)
(apply vector arg1 rest))
|
(Note: this could have been simpler, see Meng Zhang’s solution)

This will combine individual words into a vector, as in the example given, but will not work to effectively combine existing vectors or a mixture of vectors and words.
empty in vectors:
|
1
2
3
|
(define (vec-empty? vec)
(equal? vec '#()))
|

first in vectors:
|
1
2
3
|
(define (vec-first vec)
(vector-ref vec 0))
|

butfirst in vectors:
|
1
2
3
4
5
6
7
8
|
(define (vec-butfirst vec)
(butfirst-helper vec (make-vector (- (vector-length vec) 1)) 1))
(define (butfirst-helper vec newvec index)
(if (= index (vector-length vec)) newvec
(begin (vector-set! newvec (- index 1) (vector-ref vec index))
(butfirst-helper vec newvec (+ 1 index)))))
|
last in vectors:
|
1
2
3
|
(define (vec-last vec)
(vector-ref vec (- (vector-length vec) 1)))
|

butlast in vectors:
|
1
2
3
4
5
6
7
8
9
|
(define (vec-butlast vec)
(butlast-helper vec (make-vector (- (vector-length vec) 1)) 0))
(define (butlast-helper vec newvec index)
(if (= index (- (vector-length vec) 1)) newvec
(begin (vector-set! newvec index (vector-ref vec index))
(butlast-helper vec newvec (+ 1 index)))))
|

(You don’t have to make these procedures work on lists as well as vectors!)
(b) Does the following program still work with the new implementation of sentences? If not, fix the program.

For this I draw on vector-append from 23.3:
|
1
2
3
|
(define (praise stuff)
(vector-append stuff '#(is good)))
|
(Note: it’s possible they meant “make the praise procedure work specifically with your new implementation of sentence.” I found that part a bit vague. Meng Zhang patched up his solution for sentence a bit to make it work for this problem. The way he did it appears to involve taking a vector, going to a list, using list procedures, and then converting back to a vector, which I thought was against the instructions).
(c) Does the following program still work with the new implementation of sentences? If not, fix the program.

My solution:
|
1
2
3
|
(define (praise stuff)
(vector-append stuff '#(rules)))
|
(d) Does the following program still work with the new implementation of sentences? If not, fix the program. If so, is there some optional rewriting that would improve its performance?

It does not work as written cuz item expects a list. But if you use the vector procedures we’ve made it works okay:
|
1
2
3
4
5
6
|
(define (vec-item n sent)
(if (= n 1)
(vec-first sent)
(vec-item (- n 1)(vec-butfirst sent))))
|
(e) Does the following program still work with the new implementation of sentences? If not, fix the program. If so, is there some optional rewriting that would improve its performance?

It does not cuz every does not expect a vector.
The apply-fn-to-vec-elems procedure I made in 23.15 can help, though:
|
1
2
3
4
5
|
(define (apply-fn-to-vec-elems vec fn index)
(if (= index (vector-length vec)) vec
(begin (vector-set! vec index (fn (vector-ref vec index)))
(apply-fn-to-vec-elems vec fn (+ 1 index)))))
|
|
1
2
3
|
(define (vec-every fn vec)
(apply-fn-to-vec-elems vec fn 0))
|
If we have a procedure add2 that adds 2 to some argument, we can say:

(f) In what ways does using vectors to implement sentences affect the speed of the selectors and constructor? Why do you think we chose to use lists?
To take one example, for something like butfirst, with a list implementation of sentences, you can implement butfirst with cdr, which is a constant time operation that isn’t affected by the size of the list. But to implement butfirst with vectors, you need to recursively go through the list and build a new list with all but the first element, as I did above, and this will take a longer amount of time with longer lists. If you think that such operations with sentences such as butfirst will be common, that would be a reason to choose to implement sentences as lists rather than as vectors.
