The big idea in this part of the book is deceptively simple. It’s that we can take the value returned by one function and use it as an argument to another function. By “hooking up” two functions in this way, we invent a new, third function. […]
We know that this idea probably doesn’t look like much of a big deal to you. It seems obvious. Nevertheless, it will turn out that we can express a wide variety of computational algorithms by linking functions together in this way. This linking is what we mean by “functional programming.”
Chapter 3 – Expressions
Quotes from here.
Read-eval-print loop – Interaction between you and Scheme.
Scheme reads what you type, evaluates it, and prints the answer, and then does the same thing over again.
Expressions – a question you type into Scheme.
Atomic expression – a single value, such as 26.
Compound expression – an expression made out of smaller expressions, such as (+ 14 7).
Scheme versus other languages:
If you’ve programmed before in some other language, you’re probably accustomed to the idea of several different types of statements for different purposes. For example, a “print statement” may look very different from an “assignment statement.” In Scheme, everything is done by calling procedures, just as we’ve been doing here. Whatever you want to do, there’s only one notation: the compound expression.
Little People
This chapter uses a model of little people to explain how an expression like (- (+ 5 8) (+ 2 4)) gets evaluated.
A tree depicting some stuff discussed in the chapter:
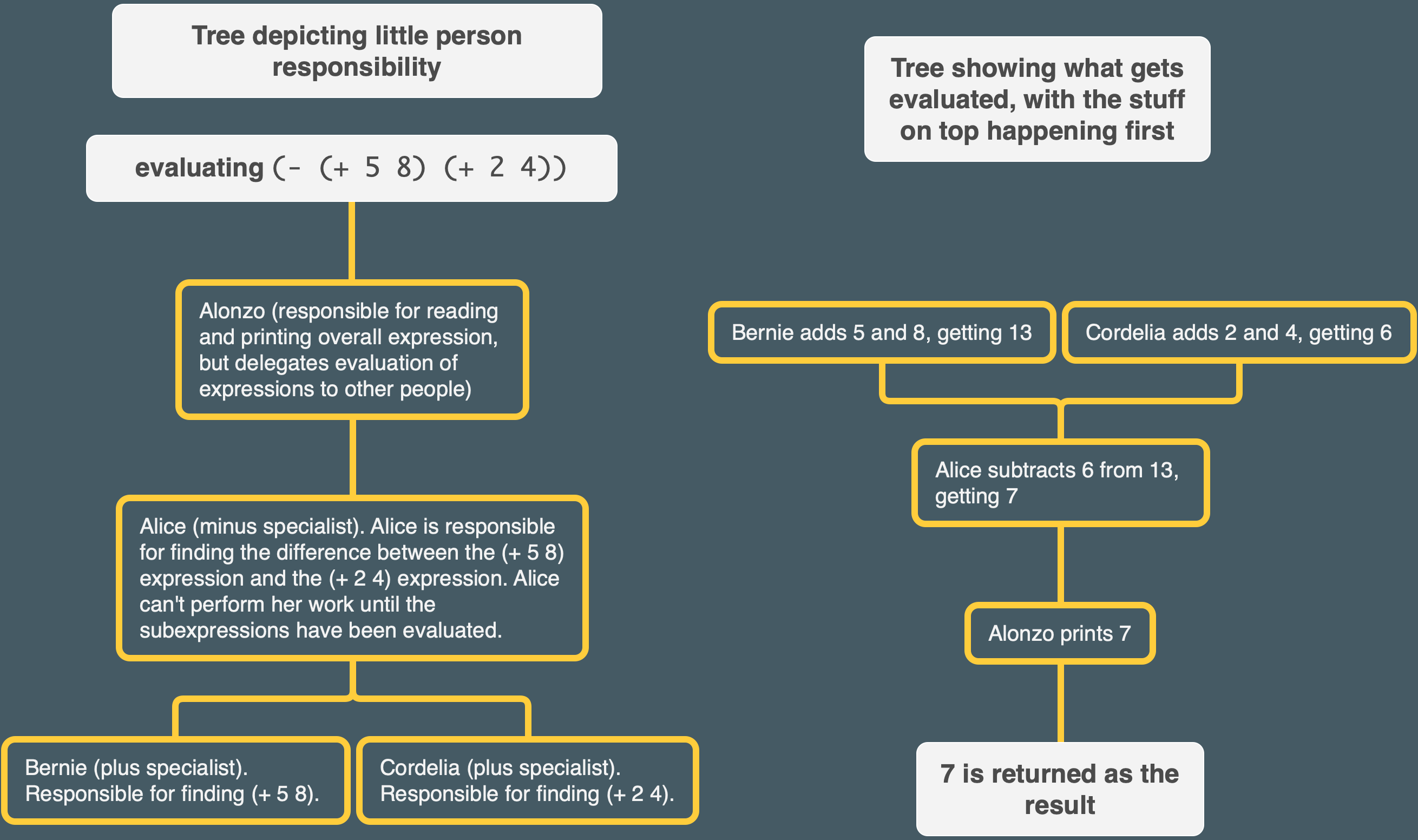
The parentheses are key for guiding the workflow:
How does Alonzo know what’s the argument to what? That’s what the grouping of subexpressions with parentheses is about. Since the plus expressions are inside the minus expression, the plus people have to give their results to the minus person.
The book has an important clarification about the descriptive model it uses:
We’ve made it seem as if Bernie does his work before Cordelia does hers. In fact, the order of evaluation of the argument subexpressions is not specified in Scheme; different implementations may do it in different orders. In particular, Cordelia might do her work before Bernie, or they might even do their work at the same time, if we’re using a parallel processing computer. However, it is important that both Bernie and Cordelia finish their work before Alice can do hers.
Bernie and Cordelia must finish their work before Alice can do hers because Alice can’t know what she’s supposed to subtract from what until Bernie and Cordelia are finished. So the very nature of Alice’s workflow is dependent upon what Bernie and Cordelia discover. However, Bernie and Cordelia’s workflows are independent from each other, so they can happen in whatever order or at the same time.
We can express this organization of little people more formally. If an expression is atomic, Scheme just knows the value.[3] Otherwise, it is a compound expression, so Scheme first evaluates all the subexpressions (in some unspecified order) and then applies the value of the first one, which had better be a procedure, to the values of the rest of them. Those other subexpressions are the arguments.
Makes sense.
(Scheme ignores everything to the right of a semicolon, so semicolons can be used to indicate comments, as above.)
Ah I’d forgotten what the indicator for comments was 🙂
Results Replacement
To keep track of which result goes into which larger computation, you can write down a complicated expression and then rewrite it repeatedly, each time replacing some small expression with a simpler expression that has the same value.
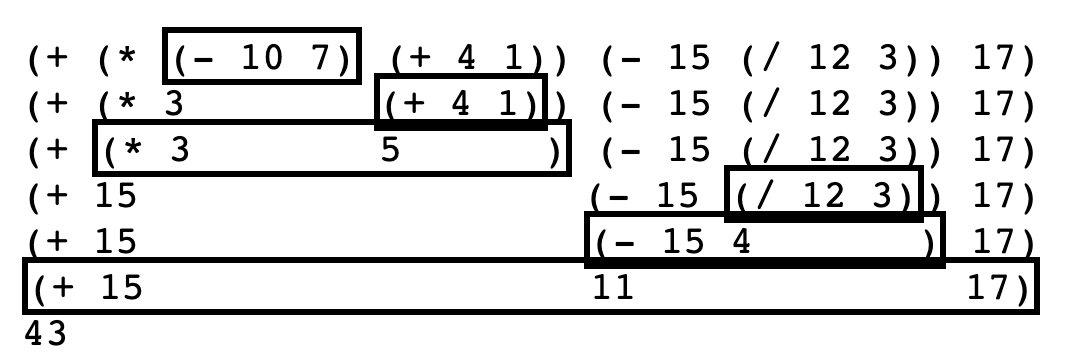
In each line of the diagram, the boxed expression is the one that will be replaced with its value on the following line.
They’re going very step-by-step here to show how the program works and avoid confusion, which is good.
If you like, you can save some steps by evaluating several small expressions from one line to the next:
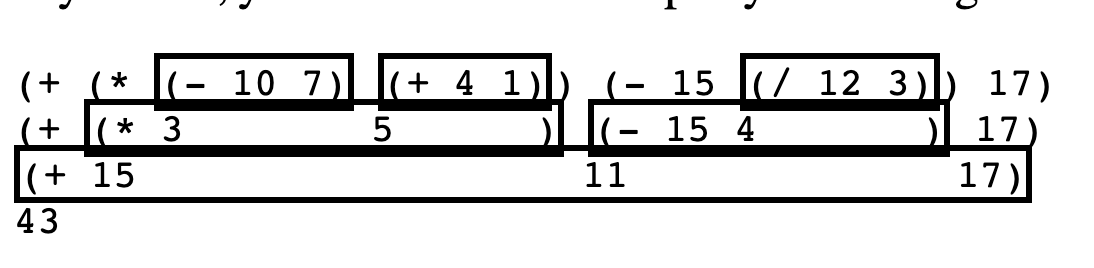
I think this is how I would do it, since only replacing one expression at a time seems pretty tedious.
Plumbing Diagrams
This section has some pictures depicting a procedure as a machine. I often think in terms of machine metaphors for procedures, especially when they do things like add or remove something to some input data. I find it easy to analogize certain programs to the sort of thing that might happen on an assembly line.
Here is Simply Scheme’s diagram for (- (+ 5 8) (+ 2 4)):
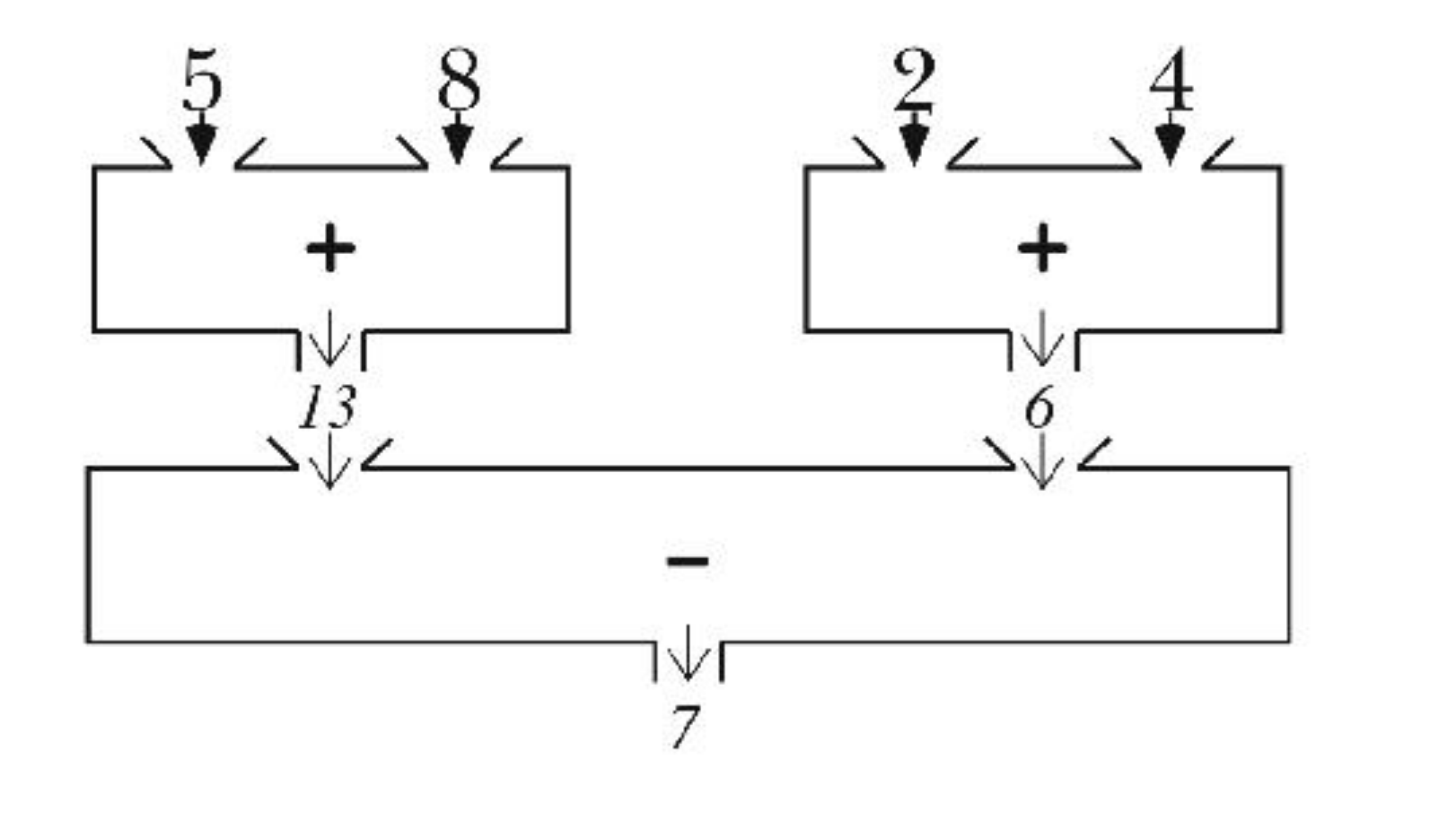
There is some similarity to the rightmost tree of the two trees I made above (though I used words).
Pitfalls
The book lists some Scheme pitfalls.
The first pitfall is people reading programs from left to right rather than thinking in terms of expressions and subexpressions. I don’t think I have that particular issue, though I can see it being a big problem. I think I found it fairly intuitive to imagine the subexpressions flowing up through the structure of the procedure as they are evaluated. I think it is particularly important to be able to think of things that way when you try to think about recursion, cuz you’ve got to think of what happens when the base case gets reached and then what happens to the result that is returned from the base case and so on.
Another pitfall is that people think Scheme cares about white space. They emphasize that they’ve been indenting things for readability but that the parentheses are what actually matters. Contrast this with Python, which does care about white space.

A consequence of Scheme’s not caring about white space is that when you hit the return key, Scheme might not do anything. If you’re in the middle of an expression, Scheme waits until you’re done typing the entire thing before it evaluates what you’ve typed.
So if you forget a paren and hit return, nothing will happen. You’ve gotta finish your expression before Scheme will try to evaluate it.
I hit enter after the following expression and you can see what Racket did – it just went to the next line but didn’t try to evaluate the expression:
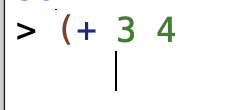
The book also mentions that stray quotation marks " can cause trouble, if you just have one and it isn’t paired off.
They also say:
One other way that Scheme might seem to be ignoring you comes from the fact that you don’t get a new Scheme prompt until you type in an expression and it’s evaluated. So if you just hit the return or enter key without typing anything, most versions of Scheme won’t print a new prompt.
Yeah, for me Racket just keeps going down a line but with no new > if I keep hitting enter, at least until I actually do something:

Exercises
Some files for this chapter are posted in my Github.
✅ Exercise 3.1
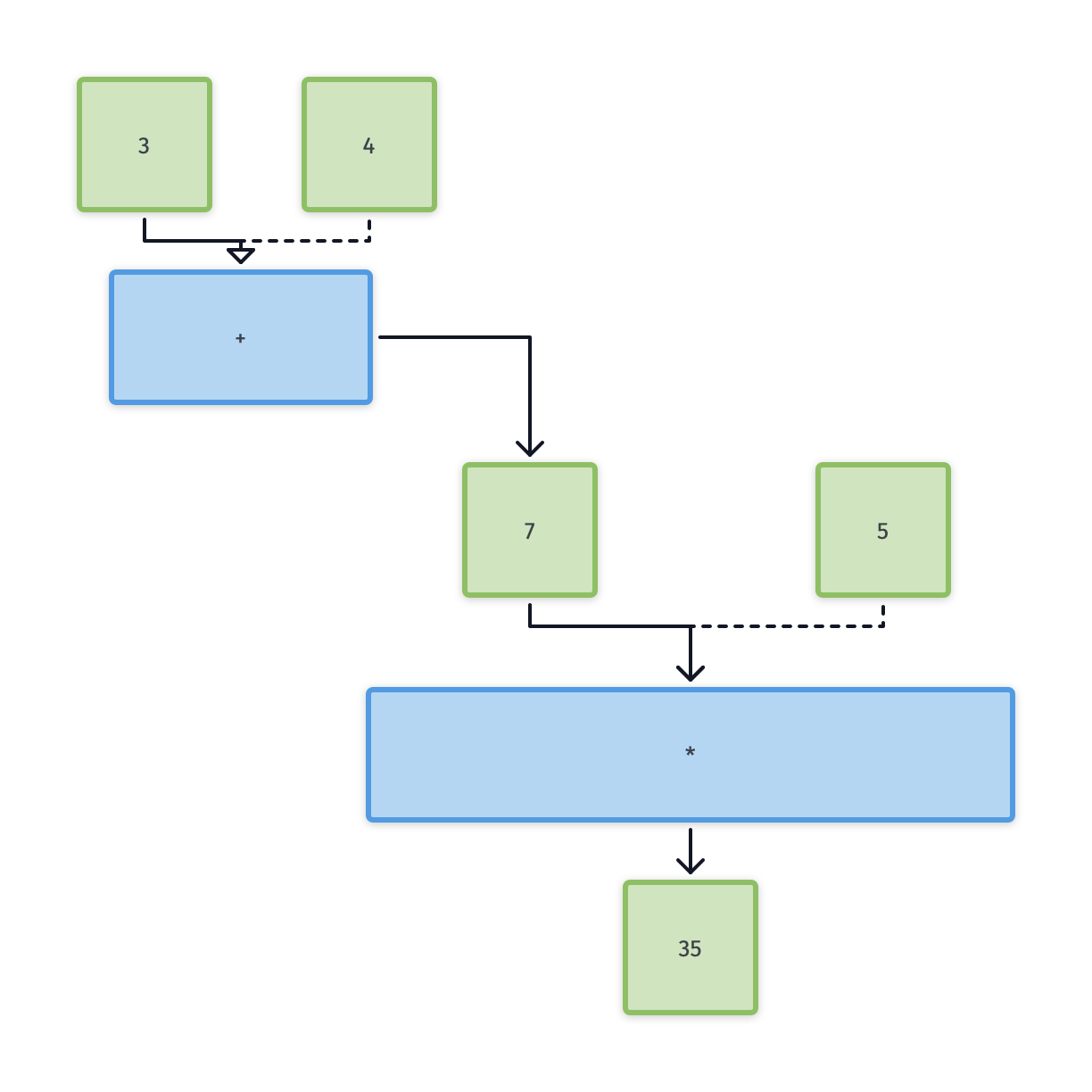
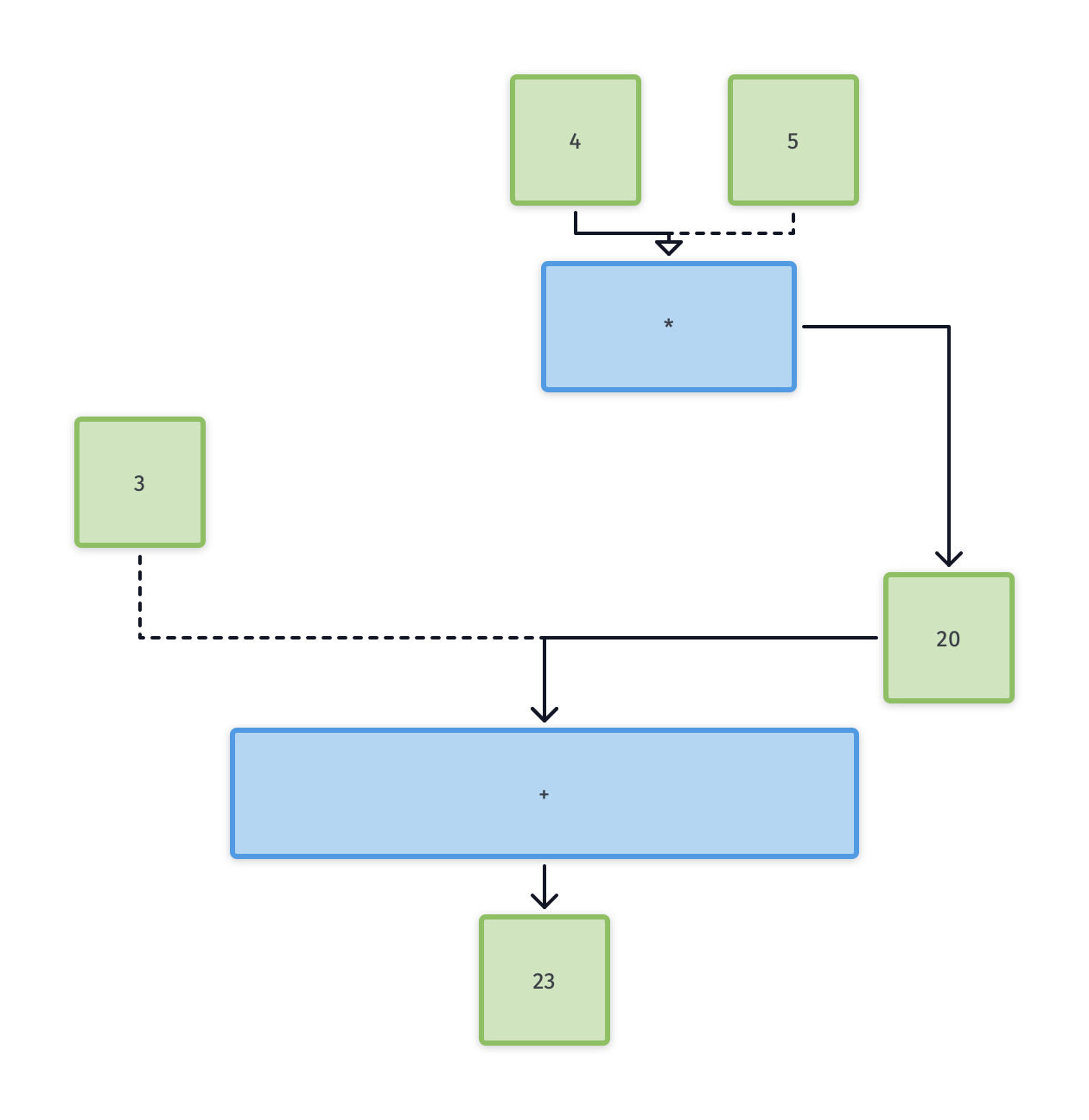
Translate the arithmetic expressions (3+4)×5 and 3+(4×5) into Scheme expressions, and into plumbing diagrams.
|
1
2
3
|
> (* (+ 3 4) 5)
35
|
my attempt at something like a plumbing diagram for the above expression:
|
1
2
3
|
> (+ 3 (* 4 5))
23
|
✅ Exercise 3.2
How many little people does Alonzo hire in evaluating each of the following expressions:
I think the way to think of this is “how many operations were performed?” So you just count up the number of operations like +, *, and -. This also matches the number of open or closing parentheses, respectively.
|
1
2
|
(+ 3 (* 4 5) (- 10 4))
|
I think there are 3 little people in this example. In this case, the + takes 3 values, but I don’t think that affects the number of little people.
|
1
2
|
(+ (* (- (/ 8 2) 1) 5) 2)
|
4 little people for this one.
|
1
2
3
4
5
6
|
(* (+ (- 3 (/ 4 2))
(sin (* 3 2))
(- 8 (sqrt 5)))
(- (/ 2 3)
4))
|
I counted 10 operations. I then cross-checked that against the number of opening parentheses and closing parentheses. One advantage of going by the number of parentheses is you can use a text editor to count those with the Find feature 🙂
NOTE: I’m generally checking my answers against AnneB’s to ensure accuracy and watch for mistakes. AnneB came out the same on this problem and said:
I think it’s the same as the number of procedures, which is the same as the number of left parentheses.
Yep 🙂 I’d only add that it’s also the number of right parentheses, since the number of parentheses have to match.
✅❌ Exercise 3.3
Each of the expressions in the previous exercise is compound. How many subexpressions (not including subexpressions of subexpressions) does each one have?
For example,
(* (- 1 (+ 3 4)) 8)
has three subexpressions; you wouldn’t count (+ 3 4).
Earlier in the chapter the book said:
(* (- (+ 5 8) (+ 2 4))
(/ 10 2))
35This says to multiply the numbers 7 and 5, except that instead of saying 7 and 5 explicitly, we wrote expressions whose values are 7 and 5. (By the way, we would say that the above expression has three subexpressions, the
*and the two arguments. The argument subexpressions, in turn, have their own subexpressions. However, these sub-subexpressions, such as (+ 5 8), don’t count as subexpressions of the whole thing.)
So it seems like we count sub-expressions by counting up the procedure and the number of arguments being passed to the procedure at the highest/final “level” of the expression.
(❌ERRONEOUS STATEMENT) So this:
(+ 3 (* 4 5) (- 10 4))
has 3 sub-expressions. (the +, an expression whose value is 20, and an expression whose value is 6.
✅EDIT/CORRECTION: I somehow forgot to count the 3! Whoops.I think maybe since I’d just written “has 3 sub-expressions” I somehow thought I’d already addressed the 3? Not sure. Thanks to AnneB for helping me catch this error by having the correct answer on her blog. Also, I think AnneB’s way of noting the sub-expressions by writing out each one is better for avoiding mistakes.
This one:
(+ (* (- (/ 8 2) 1) 5) 2)
has 3 sub-expressions: +, an expression whose value is 15, and an expression whose value is 2.
For the next one, I wanted to simplify the sub-expressions in a somewhat step-by-step way in order to check my answer. For the sub-expression (/ 2 3), when simplifying, I used the decimal notation 0.6666666666666666.
|
1
2
3
4
5
6
|
(* (+ (- 3 (/ 4 2))
(sin (* 3 2))
(- 8 (sqrt 5)))
(- (/ 2 3)
4))
|
simplifies somewhat to this:
|
1
2
3
4
5
6
|
(* (+ 1
(sin 6)
(- 8 (sqrt 5)))
(- 0.6666666666666666
4))
|
which further simplifies to this:
|
1
2
3
4
5
6
|
(* (+ 1
-0.27941549819892586
5.76393202250021)
(- 0.6666666666666666
4))
|
and finally to:
|
1
2
3
|
(* 6.484516524301284
-3.333333333333333)
|
So there are three sub-expressions.
Another way to figure out the number of sub-expressions is to look at the highlighting.

If we put the cursor on the outside of the first open parenthesis, then the whole expression highlights. The * operates at the highest “level” of the procedure, so this highlighting corresponds to the level the * operates on.

With the cursor to the left of the open parenthesis that precedes +, we see another grouping. The highlighting indicates that everything inside is one big group that gets evaluated and ultimately handed to the * at the top level. So the whole highlighted thing counts as one sub-expression.

Same idea here. The whole highlighted part ultimately only counts as one sub-expression for our *.
So there are three sub-expressions:
*
|
1
2
3
4
|
(+ (- 3 (/ 4 2))
(sin (* 3 2))
(- 8 (sqrt 5)))
|
and
|
1
2
3
|
(- (/ 2 3)
4)
|
I think that there are other ways you could figure out the number of sub-expressions. You could use trees, for example. I feel like I’m okay on this point though.
✅ Exercise 3.4
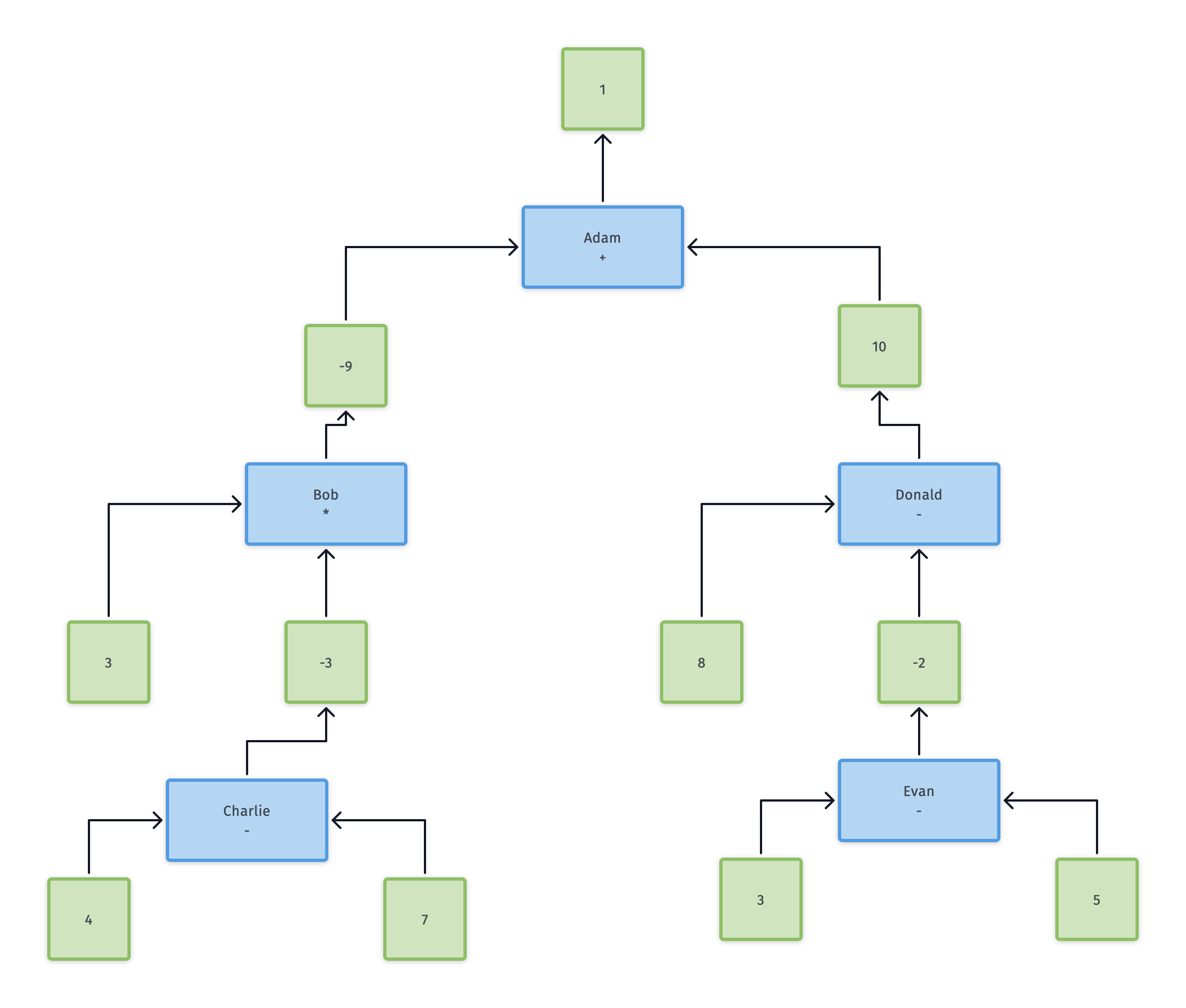
Five little people are hired in evaluating the following expression:
|
1
2
3
|
(+ (* 3 (- 4 7))
(- 8 (- 3 5)))
|
Give each little person a name and list her specialty, the argument values she receives, her return value, and the name of the little person to whom she tells her result.
- Adam: Addition specialist. Receives arguments -9 (from Bob) and 10 (From Donald). Returns 1. Highest level little person, no direct report.
- Bob: Multiplication specialist. Receives arguments 3 (directly) and -3 (from Charlie). Returns -9. Reports result to Adam.
- Charlie: Minus specialist. Receives arguments 4 and 7 directly. Returns -3. Reports result to Bob.
- Donald: Minus specialist. Receives argument values 8 (directly) and -2 (from Evan). Returns 10. Reports result to Adam.
- Evan:
Minus specialist. Receives argument values 3 and 5 directly. Returns -2. Reports result to Donald.
I made a diagram.
✅ Exercise 3.5
Evaluate each of the following expressions using the result replacement technique:
|
1
2
|
(sqrt (+ 6 (* 5 2)))
|
thing to be replaced in next line is in bold
(sqrt (+ 6 (* 5 2)))
(sqrt (+ 6 10))
(sqrt 16)
4
|
1
2
|
(+ (+ (+ 1 2) 3) 4)
|
(+ (+ (+ 1 2) 3) 4)
(+ (+ 3 3) 4)
(+ 6 4)
10
✅ Exercise 3.6
3.6 Draw a plumbing diagram for each of the following expressions:
|
1
2
|
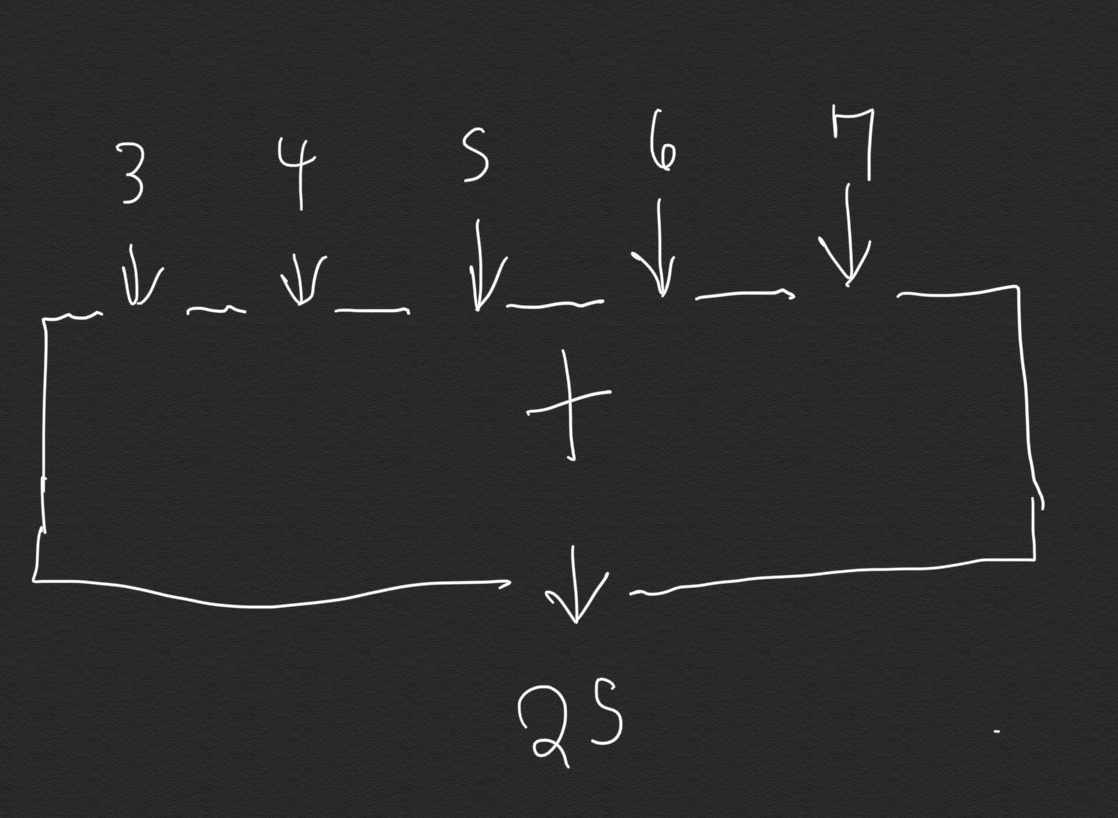
(+ 3 4 5 6 7)
|
I remembered that I have an iPad. Let’s try doing some plumbing diagrams with that
|
1
2
|
(+ (+ 3 4) (+ 5 6 7))
|
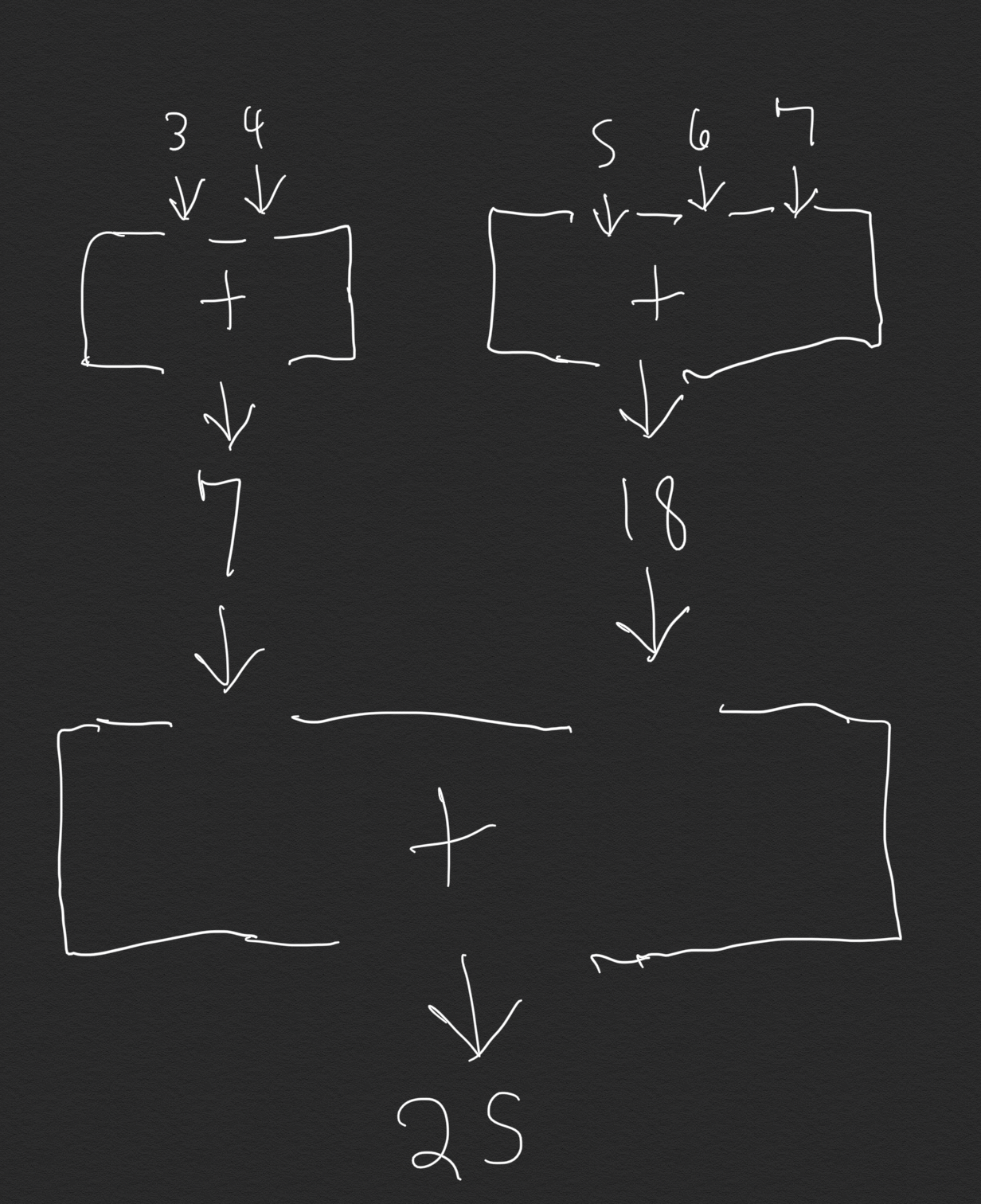
|
1
2
|
(+ (+ 3 (+ 4 5) 6) 7)
|
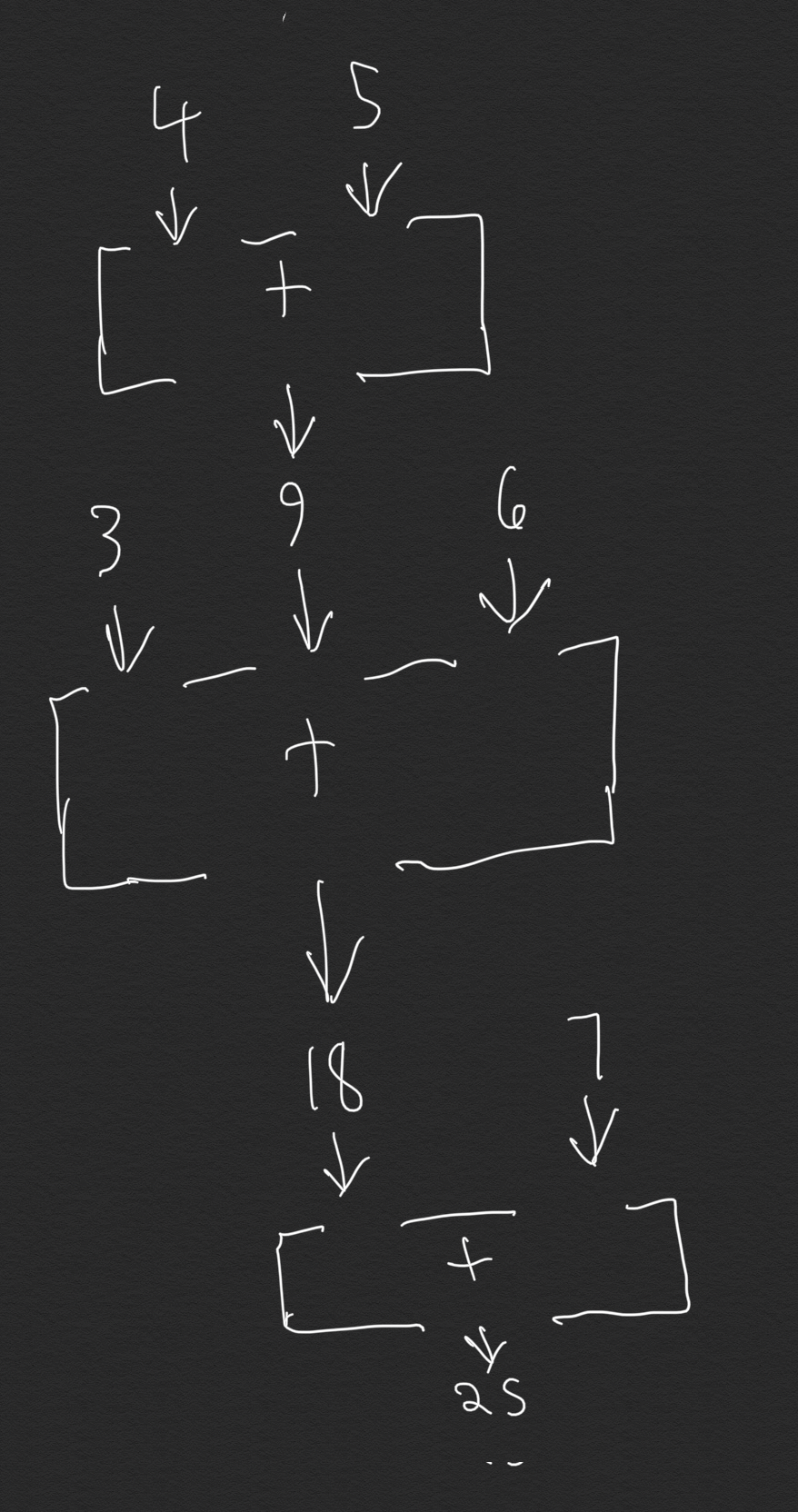
A little rough but it does the job!
✅ Exercise 3.7
What value is returned by
(/ 1 3)in your version of Scheme? (Some Schemes return a decimal fraction like0.33333, while others have exact fractional values like1/3built in.)
A fraction:

✅❌ Exercise 3.8
Which of the functions that you explored in Chapter 2 will accept variable numbers of arguments?
I checked this list from that chapter:
+, -, /, \<=, \<, =, >=, >, and, appearances, butfirst, butlast, cos, count, equal?, every, even?, expt, first, if, item, keep, last, max, member?, not, number?, number-of-arguments, odd?, or, quotient, random, remainder, round, sentence, sqrt, vowel?, and word.
I got the following list of functions:
❌INCOMPLETE:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
+
-
/
<=
<
=
>=
>
and
max
or
sentence
word
|
✅CORRECTION: AnneB noticed that random will take two arguments (and not just one) if the first argument you give it is less than the second. Strange behavior!
Also, Anne’s list is missing - and \. The behavior with these seems to be to apply the procedures to the first two arguments and then to the result of that plus the next argument, down the line until all the arguments have been dealt with.
✅ Exercise 3.9
The expression (+ 8 2) has the value 10. It is a compound expression made up of three atoms. For this problem, write five other Scheme expressions whose values are also the number ten:
• An atom
10
• Another compound expression made up of three atoms
(+ 3 7)
• A compound expression made up of four atoms
(+ 3 3 4)
• A compound expression made up of an atom and two compound subexpressions
|
1
2
|
(+ (+ 2 2) (+ 3 3))
|
• Any other kind of expression
let’s do a compound expression made up of an atom and three compound subexpressions:
|
1
2
|
(+ (+ 4 5) (+ 5 8) (+ 8 9))
|